







Hello, I'm a mathematician with a background in graph theory and combinatorics. Currently I am a postdoctoral researcher in the algorithm research group at the Université libre de Bruxelles. Here is a list of my papers on arXiv. To read summaries, you can also click on "abstract" under the publications listed below.
Consider the minimum number of colors $\chi_q(t;n)$ needed to color the points of the finite projective space $PG(n−1,q)$ such that no $(t−1)$-dimensional projective subspace is monochromatic. Via an equivalence with multicolour vector space Ramsey numbers we improve various bounds. For $\chi(n):=\chi_2(2;n)$ there is an elegant alternative interpretation: it equals the minimum number of sum-free sets that partition the nonzero elements of $\mathbb{F}_2^n$. We prove that good bounds on $\chi(n)$ for small values of $n$ imply a much better asymptotic bound. As a consequence if e.g. one could show (either by computer or with a clever idea) that $\chi(8)\le 5$ or $\chi(13)\le 8$, then it would already imply an improvement over the best-known growth rate of the multicolour Ramsey numbers for triangles, thus making progress towards the notorious Schur-Erdős problem.
If you $k$-colour the edges of a complete graph on at least $(4\ell)^k \cdot k^{k/\ell}$ vertices, then there exists a monochromatic odd cycle $H$ of length $2\ell+1$. This is the first improvement in the exponent that goes beyond an absolute constant factor since the work of Bondy and Erdős from 1973. The proof only requires that every small-radius ball in an $H$-free graph has small chromatic number.
Given a proper colouring of a graph $G$, a recolouring step changes the colour at a single vertex to another colour that is currently unused on its neighbours, hence maintaining a proper colouring.
Suppose that each vertex $v$ has its own private list $L(v)$ of allowed colours such that $|L(v)| = \deg(v)+1$.
We prove that if $G$ is connected but not a path or a cycle, then for any two proper $L$-colourings in which at least one vertex can be recoloured, one can be transformed to the other by a sequence of $O(|V(G)|^2)$ recolouring steps. Thus the space of $L$-colourings is a union of isolated vertices and a non-trivial component of small diameter.
An important ingredient of our proof is that even a single vertex $w$ with larger list size $>\deg(w)+1$ already ensures that the space of $L$-colourings becomes fully connected with diameter $O(|V(G)|^2)$, so without any isolated vertices.
We also show that a single vertex $w$ with smaller list size $<\deg(w)+1$ can already lead to situations where the space of $L$-colourings is `shattered' into arbitrarily many large components.

Our results can be interpreted as showing a sharp phase transition in the Glauber dynamics of proper $L$-colourings of graphs.
This constitutes a local strengthening and generalisation of a result of Feghali, Johnson, and Paulusma, which considered the situation where the lists are all identical to $\{1,\ldots,\Delta+1\}$.
A recolouring sequence, between k-colourings alpha and beta of a graph G, transforms alpha into beta by recolouring one vertex at a time, such that after each recolouring step we again have a proper k-colouring of G. The maximum number of required recolouring steps is the k-diameter of G. In this work we are interested in G for which the k-diameter is at most linear in the number of vertices of G.
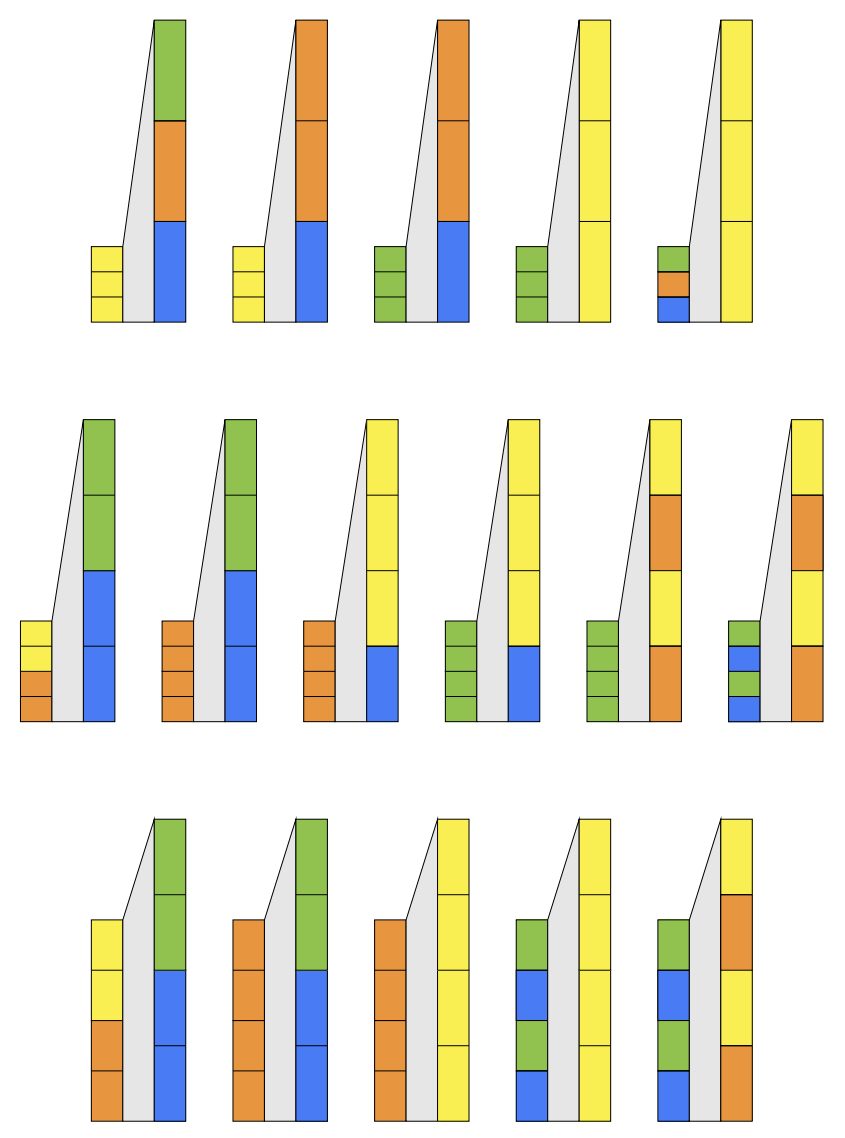 (1) We find that even for simple graphs such as complete bipartite graphs, determining the exact value of the diameter is nontrivial, and in particular we observe two phase transitions as the size of one of its parts increases.
(1) We find that even for simple graphs such as complete bipartite graphs, determining the exact value of the diameter is nontrivial, and in particular we observe two phase transitions as the size of one of its parts increases.
(2) We present an optimal version of the so-called Renaming Lemma, which has been used as a subroutine in several papers. If alpha and beta induce the same partition into colour classes, then they can be recoloured into each other in at most 3/2*|V(G)| recolouring steps. This is sharp and improves upon the often-used upper bound 2*|V(G)|.
(3) We observe that replacing k with k+1 does not have a predictable monotone effect. It does not always decrease the diameter, nor does it always increase the diameter. In the list-colouring analogue we demonstrate an even stronger variety. We are curious how extreme the fluctuations can be.
In this paper we showcase techniques to bound the fractional list-packing number $\chi_{\ell}^{\bullet}(G)$ of a graph $G$,
a recently introduced graph invariant that measures the existence of a `perfectly balanced' collection of proper colourings.
 (1) A direct consequence of our central technical lemma is that $\chi_{\ell}^{\bullet}(G)$ is at most the treedepth of $G$.
We further strengthen this by proving that $\chi_{\ell}^{\bullet}(G)$ is at most $1 +$ pathwidth of $G$.
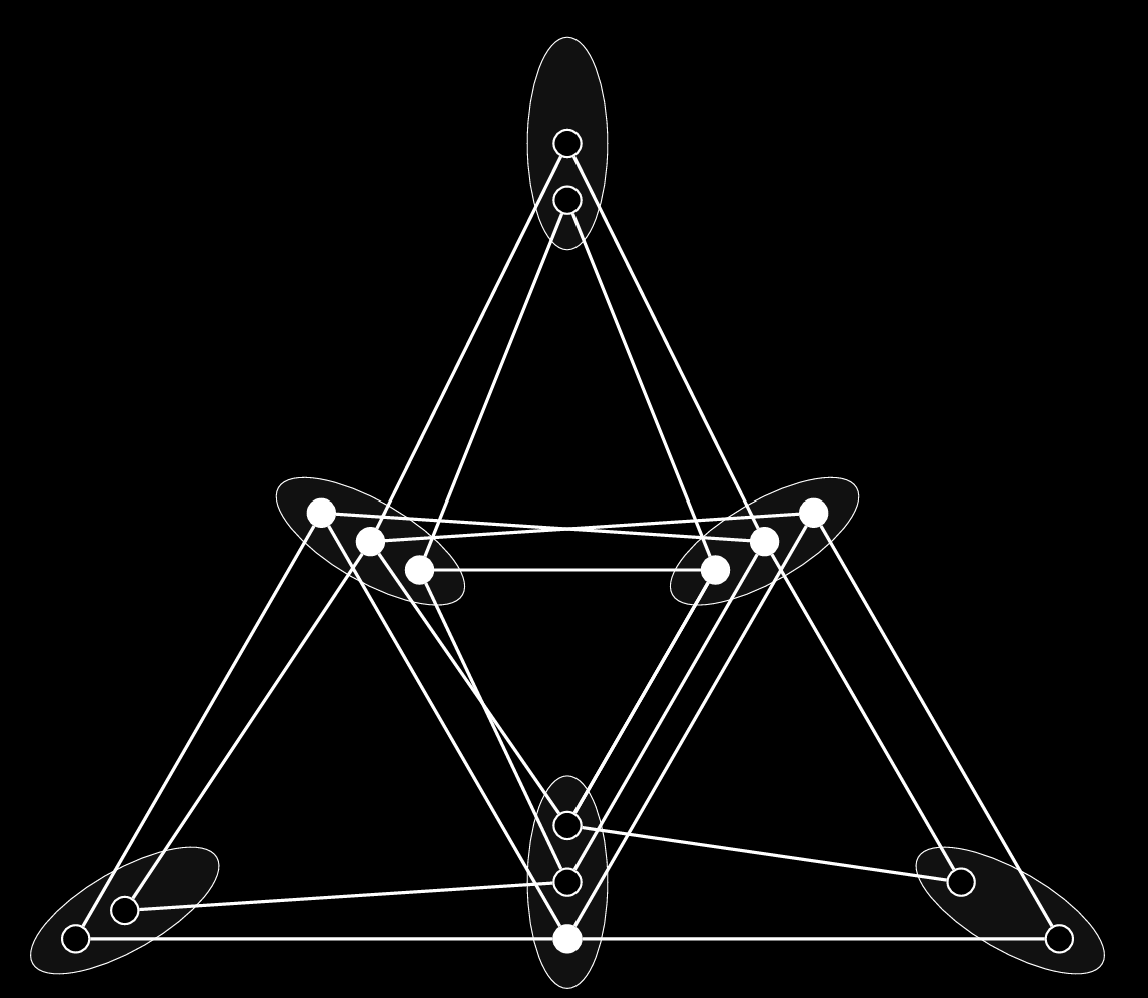
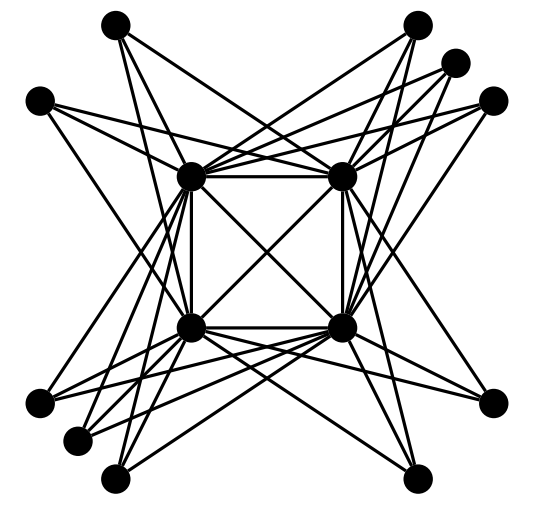
Moreover, we exhibit examples of graphs with $\chi_{c}^{\bullet}(G)$ strictly larger than $1 +$ treewidth, such as the one in the picture.
(1) A direct consequence of our central technical lemma is that $\chi_{\ell}^{\bullet}(G)$ is at most the treedepth of $G$.
We further strengthen this by proving that $\chi_{\ell}^{\bullet}(G)$ is at most $1 +$ pathwidth of $G$.
Moreover, we exhibit examples of graphs with $\chi_{c}^{\bullet}(G)$ strictly larger than $1 +$ treewidth, such as the one in the picture.
(2) It is still unknown whether $\chi_{\ell}^{\bullet}(G)$ is at most 2 plus the degeneracy of $G$, but we make a small step in this direction.
(3) We also bound $\chi_{\ell}^{\bullet}(G)$ for the Cartesian product of graphs. In particular we find that it is at most $k+1$ for the Cartesian product
of $k$ nontrivial trees, and this is tight. Previously this was only known for the Cartesian product of two paths.
We study the existence of many disjoint list-colorings of a graph, with a focus on planar graphs under various girth constraints. We also consider H-minor-free graphs, where H is some small complete or complete bipartite graph H.
Example 1: For every planar graph G and every list-assignment L with lists of size 8, there exist 8 disjoint proper L-colorings of G.
This means that at every vertex v, each of the 8 colours in its list L(v) occurs in precisely one of the 8 L-colorings.
In other words, the list-packing number of a planar graph is at most 8.
More generally, this is true for all K5-minor-free graphs, and even more generally for all graphs with maximum average degree <6.
 Example 2: For every planar triangle-free graph, the list-packing number is at most 5. More generally this is true for all graphs with maximum average degree <4.
Example 2: For every planar triangle-free graph, the list-packing number is at most 5. More generally this is true for all graphs with maximum average degree <4.
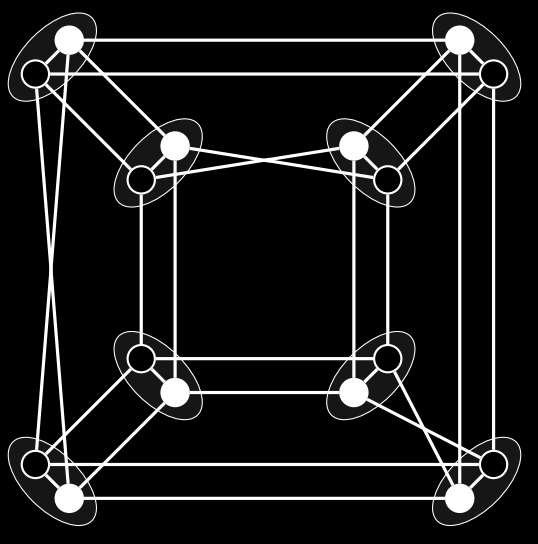
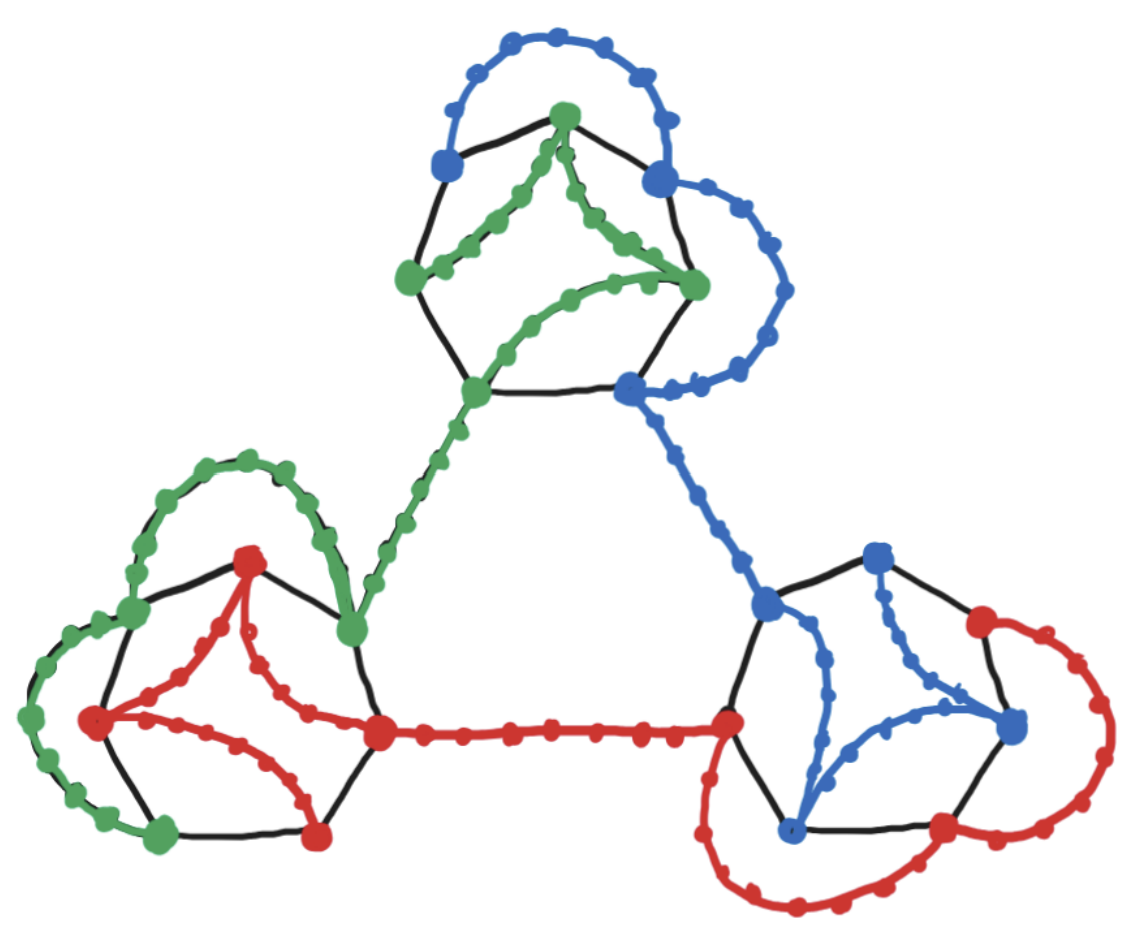
Example 3: For every planar graph with girth g>=5, the list-packing number is at most 4. This is optimal for every g>=5; see the picture for a construction attaining equality.
Example 4: Every planar graph of girth at least 6 has fractional list-packing number at most 3.
By definition, this means that for every list-assignment L with lists of size 3, there exists a probability distribution on the proper L-colorings c of G
such that at every vertex v and for every colour x in its list L(v), the probability that v is coloured x by c is 1/3.
In other words: at every vertex, every allowed colour is equally likely to appear in a proper L-coloring.
All of the above also hold for correspondence-colorings instead of list-colorings.
Furthermore, as direct corollaries we improve bounds on (weighted) epsilon-flexibility for several classes of planar graphs.
The latter is a concept which has been introduced by Dvorak, Norin and Postle (2019) to encode how much
a proper L-coloring can be made to agree with any given (not necessarily proper) preferred L-coloring.
A graph class $\mathcal{C}$ has polynomial expansion if there is a polynomial function $f$ such that for every graph $G\in \mathcal{C}$, each of the depth-$r$ minors of $G$ has average degree at most $f(r)$. In this note, we study bounded-radius variants of some classical graph parameters such as bramble number, linkedness and well-linkedness, and we show that they are pairwise polynomially related. Furthermore, in a graph class with polynomial expansion they are all uniformly bounded by a polynomial in $r$.
In our previous work we defined the list packing number of a graph, which is the least integer k such that there are always k disjoint proper list colourings whenever we have lists all of size k associated to the vertices.
We continue our investigation of how the list packing number contrasts with that of the list chromatic number, particularly in the context of bounded degree graphs.
The main question we pursue is whether every graph with maximum degree $\Delta$ has list packing number at most $\Delta + 1$.
We confirm this for small values of $\Delta$, and rather surpisingly we were also able to confirm the natural fractional relaxation for all values of $\Delta$.
While the greedy bound indeed seems to extend nicely to the setting of listpacking, we find that Books' theorem does not carry over; there are several graphs other than cliques and odd cycles with (fractional) list packing number exactly $\Delta+1$.
Minor modifications of these results also hold for a more technical variant called the correspondence packing number.
Finally, we provide examples of graphs with a list-assignment for which almost all list colourings are proper, yet no list packing exists.
The reconfiguration graph $C_k(G)$ for the $k$-colourings of a graph $G$ has a vertex for each proper $k$-colouring of $G$, and two vertices of $C_k(G)$ are adjacent precisely when those $k$-colourings differ on a single vertex of $G$. Much work has focused on bounding the maximum value of the diameter of $(C_k(G))$
over all $n$-vertex graphs $G$. We consider the analogous problems for list colourings and for correspondence colourings.
We conjecture that if $L$ is a list-assignment for a graph $G$ with $|L(v)|\ge
d(v)+2$ for all $v\in V(G)$, then diameter$(C_L(G))\le n(G)+\mu(G)$, where $\mu(G)$ denotes the matching number of $G$.
We also conjecture that if $(L,H)$ is a correspondence cover for a graph $G$ with
$|L(v)|\ge d(v)+2$ for all $v\in V(G)$, then diam $C_{(L,H)}(G)\le n(G)+\tau(G)$, where $\tau(G)$ denotes the vertex cover number
of $G$.
List colouring is an influential and classic topic in graph theory. We initiate the study of a natural strengthening of this problem, where instead of one list-colouring, we seek many in parallel.
Our explorations have uncovered a potentially rich seam of interesting problems spanning chromatic graph theory.
Given a $k$-list-assignment $L$ of a graph $G$, which is the assignment of a list $L(v)$ of $k$ colours to each vertex $v\in V(G)$, we study the existence of $k$ pairwise-disjoint proper colourings of $G$ using colours from these lists.
We may refer to this as a list-packing. Correspondingly, we define the list-packing number of $G$ as the smallest $k$ for which a list-packing is guaranteed to exist for every $k$-list-assignment of $G$.
Using a mix of combinatorial and probabilistic methods (with a central role for random binary matrices), we set out some basic upper bounds on the list-packing number, in terms of the number of vertices, the degeneracy, the maximum degree, or the (list) chromatic number of $G$.
We also pursue a more focused study of the case when $G$ is a bipartite graph.
Our results do not yet rule out the tantalising prospect that the list-packing number is uniformly bounded by a constant multiple of the list chromatic number.
Our study has taken inspiration from study of the strong chromatic number, and we also explore generalisations of the problem above in the same spirit, such as a packing variant of the correspondence chromatic number.
For instance, we find that the correspondence packing number (and hence the list-packing number) of a bipartite graph with maximum degree $\Delta$ is at most $(1+o(1)) \Delta/\log \Delta$, which is sharp up to a factor at most two.
We prove that every connected cubic graph with $n$ vertices has a maximal matching of size at most $\frac{5}{12} n+ \frac{1}{2}$. This confirms the cubic case of a conjecture of Baste, Fürst, Henning, Mohr and Rautenbach (2019) on regular graphs. More generally, we prove that every graph with $n$ vertices and $m$ edges and maximum degree at most $3$ has a maximal matching of size at most $\frac{4n-m}{6}+ \frac{1}{2}$. These bounds are attained by the graph $K_{3,3}$, but asymptotically there may still be some room for improvement. Moreover, the claimed maximal matchings can be found efficiently. As a corollary, we have a $\left(\frac{25}{18} + O \left( \frac{1}{n}\right)\right) $-approximation algorithm for minimum maximal matching in connected cubic graphs.
We wish to bring attention to a natural but slightly hidden problem, posed by Erdős and Nešetřil. in the late 1980s, an edge version of the degree-diameter problem. Our main result is that, for any graph of maximum degree $\Delta$ with more than $1.5\Delta^t$ edges, its line graph must have diameter larger than $t$. In the case where the graph contains no cycle of length $2t+1$, we can improve the bound on the number of edges to one that is exact for $t \in \left\{1,2,3,4,6\right\}$. In the case $\Delta=3$ and $t=3$, we obtain an exact bound. Our results also have implications for the related problem of bounding the distance-$t$ chromatic index, $t>2$; in particular, for this we obtain an upper bound of $1.941 \Delta^t$ for graphs of large enough maximum degree $\Delta$, markedly improving upon earlier bounds for this parameter.
We investigate the effect of a fixed forbidden clique minor upon the strong chromatic index, both in multigraphs and in simple graphs. We conjecture for each $k\ge 4$ that any $K_k$-minor-free multigraph of maximum degree $\Delta$ has strong chromatic index at most $\frac32(k-2)\Delta$. We present a construction certifying that if true the conjecture is asymptotically sharp as $\Delta\to\infty$. In support of the conjecture, we show it in the case $k=4$ and prove the statement for strong clique number in place of strong chromatic index. By contrast, we make a basic observation that for $K_k$-minor-free simple graphs, the problem of strong edge-colouring is ``between'' Hadwiger's Conjecture and its fractional relaxation. We also treat $K_k$-minor-free multigraphs of edge-diameter at most $2$.
Motivated by a conjecture of the first author, we prove that every properly coloured triangle-free graph of chromatic number $\chi$ contains a rainbow independent set of size $\lceil\frac12\chi\rceil$. This is sharp up to a factor $2$. This result and its short proof have implications for the related notion of chromatic discrepancy. Drawing inspiration from both structural and extremal graph theory, we conjecture that every triangle-free graph of chromatic number $\chi$ contains an induced cycle of length $\Omega(\chi\log\chi)$ as $\chi\to\infty$. Even if we only asked for an induced path of length $\Omega(\chi\log\chi)$, the conclusion would be sharp up to a constant multiple. We prove it for regular girth $5$ graphs and for girth $21$ graphs. As a common strengthening of the induced paths form of this conjecture and of Johansson's theorem (1996), we posit the existence of some $c>0$ such that for every forest $H$ on $D$ vertices, every triangle-free and induced H-free graph has chromatic number at most $\frac{cD}{\log D}$. We prove this assertion with triangle-free replaced by regular girth $5$.
We prove that for every integer $t\ge 1$ there exists a constant $c_t$ such that for every $K_t$-minor-free graph $G$ and every set $S$ of balls in $G$, the minimum size of a set of vertices of $G$ intersecting all the balls of $S$ is at most $c_t$ times the maximum number of vertex-disjoint balls in $S.$ This was conjectured by Chepoi, Estellon, and Vaxès in 2007 in the special case of planar graphs and of balls having the same radius.
A classic theorem of Erdős and Pósa (1965) states that every graph has either $k$ vertex-disjoint cycles or a set of $O(k \log k)$ vertices meeting all its cycles.
While the standard proof revolves around finding a large `frame' in the graph (a subdivision of a large cubic graph), an alternative way of proving this theorem is to use a ball packing argument of Kühn and Osthus (2003) and Diestel and Rempel (2005). In this paper, we argue that the latter approach is particularly well suited for studying edge variants of the Erdős-Pósa theorem.
As an illustration, we give a short proof of a theorem of Bruhn, Heinlein, and Joos (2019), that cycles of length at least $\ell$ have the so-called edge-Erdős-Pósa property. More precisely, we show that every graph $G$ either contains $k$ edge-disjoint cycles of length at least $\ell$ or an edge set $F$ of size $O(k\ell \cdot \log (k\ell))$ such that $G-F$ has no cycle of length at least $\ell$. For fixed $\ell$, this improves on the previously best known bound of $O(k^2 \log k +k\ell)$.
Every $n$-vertex planar triangle-free graph with maximum degree at most $3$ has an independent set of size at least $\frac{3}{8}n$. This was first conjectured by Albertson, Bollob\'as and Tucker, and was later proved by Heckman and Thomas. Fraughnaugh and Locke conjectured that the planarity requirement could be relaxed into just forbidding a few specific nonplanar subgraphs: They described a family $\mathcal{F}$ of six nonplanar graphs (each of order at most $22$) and conjectured that every $n$-vertex triangle-free graph with maximum degree at most $3$ having no subgraph isomorphic to a member of $\mathcal{F}$ has an independent set of size at least $\frac{3}{8}n$.
In this paper, we prove this conjecture. As a corollary, we obtain that every $2$-connected $n$-vertex triangle-free graph with maximum degree at most $3$ has an independent set of size at least $\frac{3}{8}n$, with the exception of the six graphs in $\mathcal{F}$.
This confirms a conjecture made independently by Bajnok and Brinkmann, and by Fraughnaugh and Locke.
We prove that any triangle-free graph on $n$ vertices with minimum degree at least $d$ contains a bipartite induced subgraph of minimum degree at least $d^2/(2n)$. This is sharp up to a logarithmic factor in $n$. Relatedly, we show that the fractional chromatic number of any such triangle-free graph is at most the minimum of $n/d$ and $(2+o(1))\sqrt{n/\log n}$ as $n\to\infty$. This is sharp up to constant factors. Similarly, we show that the list chromatic number of any such triangle-free graph is at most $O(\min\{\sqrt{n},(n\log n)/d\})$ as $n\to\infty$.
Relatedly, we also make two conjectures. First, any triangle-free graph on $n$ vertices has fractional chromatic number at most $(\sqrt{2}+o(1))\sqrt{n/\log n}$ as $n\to\infty$. Second, any triangle-free graph on $n$ vertices has list chromatic number at most $O(\sqrt{n/\log n})$ as $n\to\infty$.
Given a graph $G$, the strong clique number $\omega_2'(G)$ of $G$ is the cardinality of a largest collection of edges every pair of which are incident or connected by an edge in $G$. We study the strong clique number of graphs missing some set of cycle lengths. For a graph $G$ of large enough maximum degree $\Delta$, we show among other results the following:
$\omega_2'(G)\le5\Delta^2/4$ if $G$ is triangle-free;
$\omega_2'(G)\le3(\Delta-1)$ if $G$ is $C_4$-free;
$\omega_2'(G)\le\Delta^2$ if $G$ is $C_{2k+1}$-free for some $k\ge 2$.
These bounds are attained by natural extremal examples. Our work extends and improves upon previous work of Faudree, Gy\'arf\'as, Schelp and Tuza (1990), Mahdian (2000) and Faron and Postle (2019). We are motivated by the corresponding problems for the strong chromatic index.
Let $H$ be a planar graph. By a classical result of Robertson and Seymour, there is a function $f:\mathbb{N} \to \mathbb{R}$ such that for all $k \in \mathbb{N}$ and all graphs $G$, either $G$ contains $k$ vertex-disjoint subgraphs each containing $H$ as a minor, or there is a subset $X$ of at most $f(k)$ vertices such that $G-X$ has no $H$-minor. We prove that this remains true with $f(k) = c k \log k$ for some constant $c=c(H)$. This bound is best possible, up to the value of $c$, and improves upon a recent result of Chekuri and Chuzhoy (STOC 2013), who established this with $f(k) = c k \log^d k$ for some universal constant $d$. The proof is constructive and yields a polynomial-time $O(\log \text{opt})$-approximation algorithm for packing subgraphs containing an $H$-minor.
Let $G$ be a claw-free graph on $n$ vertices with clique number $\omega$, and consider the chromatic number $\chi(G^2)$ of the square $G^2$ of $G$. Writing $\chi_s^{'}(d)$ for the supremum of $\chi(L^2)$ over the line graphs $L$ of simple graphs of maximum degree at most $d$, we prove that $\chi(G^2) \leq \chi_s^{'}(\omega)$ for $\omega \in \left\{3,4\right\}$. For $\omega=3$, this implies the sharp bound $\chi(G^2) \leq 10$. For $\omega=4$, this implies $\chi(G^2) \leq 22$, which is within $2$ of the conjectured best bound. This work is motivated by a strengthened form of a conjecture of Erdős and Nešetřil.
Two graphs $G_1$ and $G_2$ on $n$ vertices are said to pack if there exist injective mappings of their vertex sets into $[n]$ such that the images of their edge sets are disjoint. A longstanding conjecture due to Bollob\'as and Eldridge and, independently, Catlin, asserts that, if $(\Delta(G_1)+1) (\Delta(G_2)+1) \le n+1$, then $G_1$ and $G_2$ pack. We consider the validity of this assertion under the additional assumption that $G_1$ or $G_2$ has bounded codegree. In particular, we prove for all $t \ge 2$ that, if $G_1$ contains no copy of the complete bipartite graph $K_{2,t}$ and $\Delta(G_1) > 17 t \cdot \Delta(G_2)$, then $(\Delta(G_1)+1) (\Delta(G_2)+1) \le n+1$ implies that $G_1$ and $G_2$ pack. We also provide a mild improvement if moreover $G_2$ contains no copy of the complete tripartite graph $K_{1,1,s}$, $s\ge 1$.
A Jordan region is a subset of the plane that is homeomorphic to a closed disk. Consider a family $\mathcal{F}$ of Jordan regions whose interiors are pairwise disjoint, and such that any two Jordan regions intersect in at most one point. If any point of the plane is contained in at most $k$ elements of $\mathcal{F}$ (with $k$ sufficiently large), then we show that the elements of $\mathcal{F}$ can be colored with at most $k+1$ colors so that intersecting Jordan regions are assigned distinct colors. This is best possible and answers a question raised by Reed and Shepherd in $1996$. As a simple corollary, we also obtain a positive answer to a problem of Hliněný ($1998$) on the chromatic number of contact systems of strings. We also investigate the chromatic number of families of touching Jordan curves. This can be used to bound the ratio between the maximum number of vertex-disjoint directed cycles in a planar digraph, and its fractional counterpart.
We study the Incipient Infinite Cluster (IIC) of high-dimensional bond percolation on $\mathbb{Z}^d$. We prove that the mass dimension of IIC almost surely equals $4$ and the volume growth exponent of IIC almost surely equals $2$.
I have a University Teaching Qualification. In principle, this diploma is required to teach at a Dutch university. Completion of the necessary courses (on Course Design, Teaching, Supervision, Assessment, and Final Presentation) typically takes 1 to 2 years.
At Université libre de Bruxelles and then TU Delft, I lectured for the following courses:
Supervision at TU Delft:
As a student at Leiden University (until 2013) and then as a PhD student at Radboud University (until 2017), I taught exercise classes for the following courses: